The code used for both parts of this project can be found here

Applying the Q-Learning Algorithm to a custom environment

In the previous article, we built the standard Q-learning algorithm from scratch and implemented it as a class, Q. In this article we will construct a simple environment and attempt to solve it using the Q class.

The Environment

A device shoots a projectile from the ground toward a target that is also at ground level. The shooter is initialized with a default initial velocity (we'll set this to 15m/s but you can change it if you want). Assuming acceleration due to gravity (g) is 9.8m/s², given a discrete target distance, determine the nearest available angle (in degrees) the projectile should be jetted at.

Note: We also supply the target range. The standard q-learning algorithm is commonly applied to discrete state and action spaces so it is more intuitive to provide whole number target values (and thus whole number states)

Also, in this environment, there are nine angles available: 5°, 10°, 15°, 20°, 25°, 30°, 35°, 40° and 45°

How might we solve this task?

Designing the state and action space

The environment itself will be implemented as a subclass of Env provided by the openai gym library. The gym library is a popular resource used to write environments in code for agents to interact with. It provides popular environments for testing algorithms and gives you the tools to create your custom environments.

The advantage of subclassing Env is that by only overriding only the necessary methods, we can still solve our custom environment using baseline algorithms from other libraries designed with the gym.Env class in mind.

The State space

This is a simple environment. The states will simply be discrete values representing the target distances. Thus, I use the Box data structure provided in the gym.spaces sublibrary. Box is essentially an array that allows you to specify the lower and upper bounds for each dimension, as well as the shape and data type of the array. To understand this data structure better, consult the documentation. The documentation is also a good starting point to get familiar with other spaces provided in the gym universe.

The state space is defined in the __init__ method below. Look for the line:

self.observation_space = Box(low=target_low, high=target_high, shape=(1,), dtype=np.int32)

The __init__ method, a dunder (or magic method, as special methods like it are called in Python), is a special method that is called when an object of a class is instantiated. By passing the values target_low and target_high as instantiation parameters to the environment object, you set the bounds of the state space. By default, the default values are 3 and 22, meaning the target values to learn the angles for range from 3m to 22m.

The Action space

Similarly, the action space will be discrete, representing the angles to choose from. The action space will be represented by the Discrete data structure, which is simply a finite array that begins at 0 and ends at the provided argument for `n`. There are a couple differences between Discrete and Box such as that Discrete strictly contains integer values, is of dimension 1 and starts at 0. Box on the other hand can handle multiple data types, can be multidimensional and allows you to set different bound values for each dimension.

Note: I used the Box data structure for the state space because I wanted it to be possible to have a non-zero lower target range i.e the user can determine that the lower target range is 100m.

The documentation for Discrete can be found here

I set up the action space using these lines in the __init__ method:

self.action_space = Discrete(9)

self.action_to_angle = {
    0:5,
    1:10,
    2:15,
    3:20,
    4:25, 
    5:30, 
    6:35, 
    7:40,
    8:45
  }

The attribute action_to_angle will serve as a lookup for converting supplied action values to angles.

The reward scheme

Since Q-learning is a value-based algorithm and obtains its policy indirectly using an action-value table, we need to come up with a scheme to encourage choosing the right angle.

There are maybe better ways to do this, but I decided to go with this scheme:

Calculate error as the absolute distance between the target distance and the range covered by the projectile
Create a dictionary to store the lowest errors attained at each supplied target value
If the angle supplied during a timestep results in reducing the minimum error achieved for that target/state, the reward for that timestep is +1. If the error is greater, the reward is -1. If there is no change in the minimum error for that target value, the reward is simple, 0.😐

This way, the policy indirectly trained will be to either reduce the error, or supply the angle that achieved the lowest error.

Having explained the design of this environment, let's get into the code.

Importing libraries

from gym import Env
import numpy as np
from gym.spaces import Discrete, Box
import matplotlib.pyplot as plt
%matplotlib inline
import random

Initialization

Much of the initialization code has been explained above.

In addition, an attribute max_repeat is created. max_repeat represents the maximum number of times a target value will be repeated when step is called. If max_repeat is set to 4 and the current target is 5m, you will need to call the step method 4 times to move on to the next target value. This allows us perform more Q-Table updates for each target during an episode.

A dictionary min_error is created to store the minimum absolute errors attained for each target.

Also, a dict target_to_state is created which will be used to convert the target distance to a state value, for the Q-Table.

def __init__(self, initial_velocity=15, g=9.8, target_low=3, target_high=22, max_repeat=9):
  self.name = 'Projectile'
  # define environment bounds
  self.observation_space = Box(low=target_low, high=target_high, shape=(1,), dtype=np.int32)

  # there are 9 actions corresponding to the interval of angles from 5 to 45
  self.action_space = Discrete(9)

  # store these for easy access later
  self.n_actions = self.action_space.n
  self.n_states = target_high - target_low + 1

  self.v = initial_velocity # the default value for initial_velocity is 15m/s
  self.g = g # the default value for acceleration due to gravity is 9.8m/s²
  
  # the number of times to repeat a target value before moving on to the next
  self.max_repeat = max_repeat 

  # for action-to-angle conversion
  self.action_to_angle = {
      0:5,
      1:10,
      2:15,
      3:20,
      4:25, 
      5:30, 
      6:35, 
      7:40,
      8:45
  }

  # create a lookup of discrete state values corresponding to target distances
  self.target_to_state = {i:x for x,i in enumerate((range(target_low, target_high+1)))}

  # keep track of the lowest error attained for each target
  self.min_error = {x:np.inf for x in range(self.observation_space.low[0], self.observation_space.high[0] + 1)}

Reset

The reset() method is called to reset the state of an environment. Our reset() method

creates an attribute target_list which is an array of all the target distances and shuffles the elements. It does this so we can keep track of the current episode's arrangement of target values.
selects an initial target and removes it from target_list, using the new_target() method
initializes the range of the projectile to 0, because we are yet to take an action
initializes an attribute current_countdown for that target. current_countdown starts at the value of max_repeat and is reduced at each time step by 1. When it eventually becomes 0, a new target will be supplied
sets the done attribute to False. done becomes true when the episode is over
returns the current observation using self.get_obs() and the current error calculated by self.get_info()

def new_target(self):
  # pick a target from the list of targets and remove it 
  self.target = self.target_list.pop()
    

def get_obs(self, verbose=False):
    # self.target = self.observation_space.sample() # generate random target
    self.state = self.target_to_state[self.target] # represent target as state

    # if verbose=True, return the true value of the target distance, else return 
    # its representation as a state value
    if verbose:
        return f'Target distance: {self.target}m'
    else:
        return self.state


def get_info(self, verbose=True):
    # return the number of meters by which we've missed the target
    self.error = np.abs(self.target - self.range) # absolute error

    # if verbose=True, return a full sentence, else just return the value of the error
    if verbose:
        return f'Error: {self.error:.2f}m'
    else:
        return self.error

def reset(self, verbose=True):
    # store the set of targets we can select from 
    self.target_list = list(range(self.observation_space.low[0], self.observation_space.high[0] + 1))

    random.shuffle(self.target_list) # shuffle the available targets

    self.new_target() # generate a target value
    
    self.range = 0 # the projectile is yet to be shot, so range is still 0
    self.current_countdown = self.repeat_count # start the countdown for the current target
    self.done = False

    return self.get_obs(verbose), self.get_info()

Calculating the Range

The range (also known as horizontal distance) of the projectile is calculated using the standard formula for a projectile's range, assuming no air resistance and that the final height of the projectile is equal to its initial height: 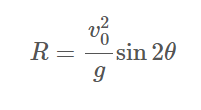Formula for the range of a projectile The angle, θ, is converted to radians from degrees.

def calc_range(self):
    # calculate the range of the projectile using the relation v²·sin(2θ)/g
    rad = np.pi/180 * angle
    range = (v**2) * np.sin(2 * rad) / g
    return range

Step

Calling step decrements current_countdown by 1. It takes an action value and calculates the range by calling calc_range(). The error is computed using get_info().

The reward is calculated using the scheme above. If the current_countdown is 0, a new target value is generated using new_target and current_countdown is reinitialized to the value of max_repeat. Once we run out of target values, done is set to True, ending the episode.

def step(self, action):
    # print(target_list)
    # reduce the target repeat countdown by 1
    current_countdown -= 1

    # map the action to the angle of projectile
    angle = action_to_angle[action]

    # this is the range covered by the projectile at the given angle, save it in the 
    # lookup table for current ranges
    range = calc_range()

    # evaluate error for this round
    error = get_info(verbose=False) 

    # if the error in this round is less than the history of errors for this round, the 
    # reward is set to +1. If it is higher, -1. Else, the reward is 0
    if error < min_error[target]:
        reward = 1 
        min_error[target] = error # update error range value
    elif error > min_error[target]:
        reward = -1
    elif error == min_error[target]:
        reward = 0

    if current_countdown == 0:
        if len(target_list) == 0:
            # set done to True when there are no values left in target_list and end episode
            done = True
        else:
            # else supply a new target and start the repeat counter again
            new_target()
            current_countdown = max_repeat
    
    return get_obs(), reward, done, get_info()

Rendering

render() contains the logic to visualize the target, range and error, using the numpy library to calculate displacement values and matplotlib library for visualization.

def render(target, angle):
    v, g = 15, 9.8 # initialize velocity and acceleration due to gravity
    rad = np.pi/180 * angle
    plt.figure()
    params = {'mathtext.default': 'regular' }  # mathtext, for subscripting 0 in v0 in plot title
    tmax = (2 * v) * np.sin(rad) / g # calculate time of flight
    t = tmax*np.linspace(0,1,100) # divide time of flight into 100 uniform time steps
    x = ((v * t) * np.cos(rad)) # horizontal distance at each time step
    y = ((v * t) * np.sin(rad)) - ((0.5 * g) * (t ** 2)) # vertical distance 

    plt.plot(x, y, color='g') # plot path

    # draw line to target target (i.e desired distance) saved in `target`
    plt.axvline(x = target, ls='--', color = 'b', label = f'target: {target}m') 

    # draw projectile at final coordinates
    plt.scatter(x[-1], y[-1], color='r', markerinitial_velocity="^", s=200)

    plt.ylim([0,10])
    plt.xlim(left=0)
    plt.title(f'$v_{0}$ = {v}m/s, θ = {angle}°, abs. error = {np.abs(x[-1]-target):.2f}m')
    plt.legend()

render(target=15, angle=30)

Putting it all together in a class: `Projectile`

class Projectile(Env):
    def __init__(self, initial_velocity=15, g=9.8, target_low=3, target_high=22, max_repeat=9):
        self.name = 'Projectile'
        # define environment bounds
        self.observation_space = Box(low=target_low, high=target_high, shape=(1,), dtype=np.int32)

        # there are 9 actions corresponding to the interval of angles from 5 to 45
        self.action_space = Discrete(9)

        # store these for easy access later
        self.n_actions = self.action_space.n
        self.n_states = target_high - target_low + 1

        self.v = initial_velocity # the default value for initial_velocity is 15m/s
        self.g = g # the default value for acceleration due to gravity is 9.8m/s²
        
        # the number of times to repeat a target value before moving on to the next
        self.max_repeat = max_repeat 

        # lookup the angle values for each action
        self.action_to_angle = {
            0:5,
            1:10,
            2:15,
            3:20,
            4:25, 
            5:30, 
            6:35, 
            7:40,
            8:45
        }

        # create a lookup of discrete state values corresponding to target distances
        self.target_to_state = {i:x for x,i in enumerate((range(target_low, target_high+1)))}

        # keep track of the lowest error attained for each target
        self.min_error = {x:np.inf for x in range(self.observation_space.low[0], self.observation_space.high[0] + 1)} 


    def new_target(self):
        # pick a target from the list of targets and remove it 
        self.target = self.target_list.pop()
        

    def get_obs(self, verbose=False):
        # self.target = self.observation_space.sample() # generate random target
        self.state = self.target_to_state[self.target] # represent target as state

        # if verbose=True, return the true value of the target distance, else return 
        # its representation as a state value
        if verbose:
            return f'Target distance: {self.target}m'
        else:
            return self.state


    def get_info(self, verbose=True):
        # return the number of meters by which we've missed the target
        self.error = np.abs(self.target - self.range) # absolute error

        # if verbose=True, return a full sentence, else just return the value of the error
        if verbose:
            return f'Error: {self.error:.2f}m'
        else:
            return self.error

    def reset(self, verbose=True):
        # store the set of targets we can select from 
        self.target_list = list(range(self.observation_space.low[0], self.observation_space.high[0] + 1))

        random.shuffle(self.target_list) # shuffle the available targets
        self.new_target() # generate a target value
        self.range = 0 # the projectile is yet to be shot, so range is still 0
        self.current_countdown = self.max_repeat # start the countdown for the current target
        self.done = False

        return self.get_obs(verbose), self.get_info()


    def calc_range(self):
        # calculate the range of the projectile using the relation v²·sin(2θ)/g
        rad = np.pi/180 * self.angle
        range = (self.v**2) * np.sin(2 * rad) / self.g
        return range

    def step(self, action):
        # print(self.target_list)
        # reduce the target repeat countdown by 1
        self.current_countdown -= 1

        # map the action to the angle of projectile
        self.angle = self.action_to_angle[action]

        # this is the range covered by the projectile at the given angle, save it in the 
        # lookup table for current ranges
        self.range = self.calc_range()

        # evaluate error for this round
        self.error = self.get_info(verbose=False) 

        # if the error in this round is less than the history of errors for this round, the 
        # reward is set to +1. If it is higher, -1. Else, the reward is 0
        if self.error < self.min_error[self.target]:
            self.reward = 1 
            self.min_error[self.target] = self.error # update error range value
        elif self.error > self.min_error[self.target]:
            self.reward = -1
        elif self.error == self.min_error[self.target]:
            self.reward = 0

        if self.current_countdown == 0:
            if len(self.target_list) == 0:
                # set self.done to True when there are no values left in self.target_list and end episode
                self.done = True
            else:
                # else supply a new target and start the repeat counter again
                self.new_target()
                self.current_countdown = self.max_repeat
        
        return self.get_obs(), self.reward, self.done, self.get_info()
        

    def render(self):
        rad = np.pi/180 * self.angle
        plt.figure()
        # plt.clf()
        params = {'mathtext.default': 'regular' }  # mathtext, for subscripting 0 in v0 in plot title
        tmax = (2 * self.v) * np.sin(rad) / self.g # calculate time of flight
        t = tmax*np.linspace(0,1,100) # divide time of flight into 100 uniform time steps
        self.x = ((self.v * t) * np.cos(rad)) # horizontal distance at each time step
        self.y = ((self.v * t) * np.sin(rad)) - ((0.5 * self.g) * (t ** 2)) # vertical distance 

        plt.plot(self.x, self.y, color='g') # plot path

        # draw line to target target (i.e desired distance) saved in `self.target`
        plt.axvline(x = self.target, ls='--', color = 'b', label = f'target: {self.target}m') 

        # draw projectile at final coordinates
        plt.scatter(self.x[-1], self.y[-1], color='r', marker="^", s=200)

        plt.ylim([0,10])
        plt.xlim(left=0)
        plt.title(f'$v_{0}$ = {self.v}m/s, θ = {self.angle}°, abs. error = {np.abs(self.x[-1]-self.target):.2f}m')
        plt.legend()
    
    def __repr__(self):
        return f'''Projectile environment: 
                    Initial velocity: {self.v}m/s
                    Acceleration due to gravity: {self.g}m/s²
                    Available angles in degrees:{list(self.action_to_angle.values())}'''

Solving this environment using the `Q` class

Using the range formula provided earlier, we can expect our Q-learning algorithms to learn the closest angles.
The table below contains actual values of the ranges covered at the provided angles

angle(°)	Range(m/s)
5°	3.98682
10°	7.8525
15°	11.4796
20°	14.7579
25°	17.5878
30°	19.8832
35°	21.5746
40°	22.6104
45°	22.9592

Let's import the Q class defined in the previous article

from q_learning import Q

Let's train, applying the Q class to the Projectile environment

sim = Projectile()
sim.reset()
model = Q(sim, exploration_fraction=0.5)
model.train()
model.show(save_as='converged.png')

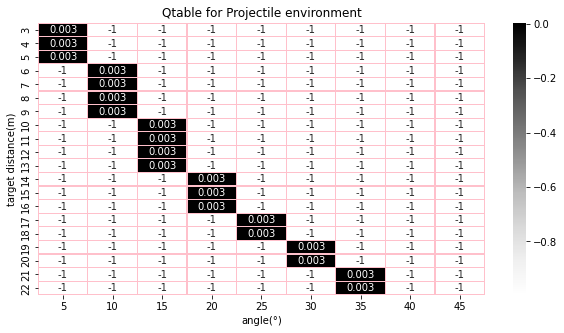
Great! Comparing the actions chosen by the algorithm after training to the correct values in the table above, we see we've been able to solve this toy problem using standard Q-Learning.